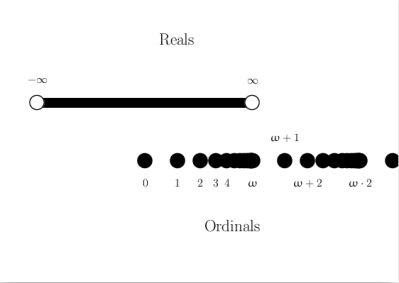
This is about the ordinal numbers, which (except for the finite ones) are less well known than the real numbers, although theoretically simpler.
The numbers of either kind compose a linear order: they can be arranged in a line, from less to greater. The orders have similarities and differences:
- Of real numbers,
- there is no greatest,
- there is no least,
- there is a countable dense set (namely the rational numbers),
- every nonempty set with an upper bound has a least upper bound.
- Of ordinal numbers,
- there is no greatest,
- every nonempty set has a least element,
- those less than a given one compose a set,
- every set has a least upper bound.
Note. Would it be helpful to write that more verbosely?
- There is no greatest real number.
- There is no least real number.
- The set of real numbers has a countable dense subset, namely the set of rational numbers.
- Every set of real numbers that has an upper bound has a least upper bound.
- There is no greatest ordinal number.
- There is a least ordinal number.
- Indeed,
- every nonempty set of ordinal numbers has a least element, and
- the class of ordinals that are less than a given ordinal is a set.
- Every set of ordinals has a least upper bound.
One can conclude in particular that the ordinals as a whole do not compose a set; they are a proper class. This is the Burali-Forti Paradox.