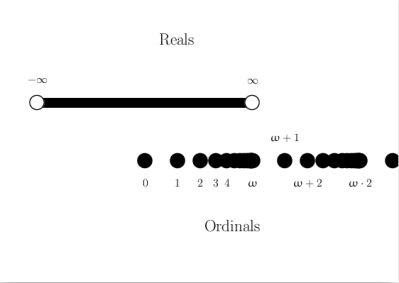
This is a little about mathematics, and a little about writing for the web, but mostly about the nuts and bolts of putting mathematics on the web. I want to record how, mainly with the pandoc program, I have converted some mathematics from a LaTeX file into html. Like “Computer Recovery” then, this post is a laboratory notebook.
In the fall of 2017, I created what I propose to consider as being both art and mathematics. Call the art conceptual; the mathematics, expository; here it is, as a booklet of 88 pages, size A5, in pdf format.
More precisely, the work to be considered as both art and mathematics is the middle of the three chapters that make up the booklet. The first chapter is an essay on art, ultimately considering some examples that inspire my own. The last chapter establishes the principle whereby the lists of numbers in Chapter 2 are created.
This past spring (of 2020), when my university in Istanbul was closed (like all others in Turkey) against the spread of the novel coronavirus, I created for my students an exercise, to serve at least as a distraction for those who could find distraction in learning.
From Weeks & Adkins, Second Course in Algebra, p. 395
Note added, April 17, 2023: An account of the mathematics involved in the exercise would ultimately be published as: Pierce, D. (2021). “Conics in Place.” Annales Universitatis Paedagogicae Cracoviensis | Studia Ad Didacticam Mathematicae Pertinentia, 13, 127–150.
This reviews some reading and thinking of recent weeks, pertaining more or less to the title subjects, of which it may be worth noting that
Summary added August 23, 2020: Mathematics may bring out such emotions as poetry does; but in the ideal, a work of mathematics is correct or not, in a sense that everybody will agree on. Here I review work of
A Twitter friend living here in Istanbul announced (on June 16) her pleasure in having a memoir published in Meanjin.
To do injustice is worse than to suffer it. Socrates proves this to Polus and Callicles in the dialogue of Plato called the Gorgias.
I wish to review the proofs, because I think they are correct, and their result is worth knowing.
Or is the result already clear to everybody?
Whom would you rather be: a Muslim in India, under attack by a Hindu mob, or a member of that mob?
You would rather not be involved; but if you had to choose, which option would be less bad: to be driven to an insane murderous fury, or to be the object of that fury?
Because Herman Wouk was going to put physicists in a novel, Richard Feynman advised him to learn calculus: “It’s the language God talks.” I think I know what Feynman meant. Calculus is the means by which we express the laws of the physical universe. This is the universe that, according to the mythology, God brought into existence with such commands as, “Let there be light.” Calculus has allowed us to refine those words of creation from the Biblical account. Credited as a discover of calculus, as well as of physical laws, Isaac Newton was given an epitaph (ultimately not used) by Alexander Pope:
Nature and Nature’s laws lay hid in night:
God said, Let Newton be! and all was light.
I don’t know, but maybe Steven Strogatz quotes Pope’s words in his 2019 book, Infinite Powers: How Calculus Reveals the Secrets of the Universe. This is where I found out about Wouk’s visit with Feynman. I saw the book recently (Saturday, February 22, 2020) in Pandora Kitabevi here in Istanbul. I looked in the book for a certain topic that was of interest to me, but did not find it; then I found a serious misunderstanding.
This is about the ordinal numbers, which (except for the finite ones) are less well known than the real numbers, although theoretically simpler.
The numbers of either kind compose a linear order: they can be arranged in a line, from less to greater. The orders have similarities and differences:
Note. Would it be helpful to write that more verbosely?
One can conclude in particular that the ordinals as a whole do not compose a set; they are a proper class. This is the Burali-Forti Paradox.
Note added, March 10–11, 2021. The bulk of this post concerns race in the theory of history, particularly the theory attributed to Johann Gottfried Herder (1744–1803). Not having read Herder for myself, I rely on the accounts of
Somebody like Herder may introduce race as an hypothesis to explain history, but ultimately the hypothesis fails, by denying us the freedom that is essential to history as such. Nonetheless, Forster defends Herder as having
an impartial concern for all human beings … Herder does also insist on respecting, preserving, and advancing national groupings. However, this is entirely unalarming,
because, for one thing, “The ‘nation’ in question is not racial but linguistic and cultural.”
Change Collingwood’s word “race” to “linguistic and cultural grouping” then. I think his conclusion remains sound: “Once Herder’s theory of race is accepted, there is no escaping the Nazi marriage laws.”
More detail is in the post below. I go on to review the philosophy of history that Collingwood presents in the Introduction of The Idea of History. This book provided me with a title for the post.
I wrote a lot in this post, as I often do. Growing self-conscious for being opinionated about the theory of history, I listed the published evidence of my actually being an historian (an historian of ancient Greek mathematics in particular).
I originally wrote that my research had been inspired by a tweet. The author of that tweet also wrote the nice long comment on this post. However, although the tweet can be found on the Internet Archive, the author later deleted his Twitter account, and so the tweet appears on Twitter today as a gap in the thread above my own tweet in response to the other tweet.
That missing tweet referred to another tweet of the author, but the Internet Archive seems not to have saved it. It did save the present post; so if one were curious, one could see the changes that I have made since initial publication, or rather since September 29, 2020, when the Archive took the first snapshot.
The changes are for style and local clarity. Any large-scale changes would need me to recover the spirit that possessed me when I originally wrote.
I return to this post now, simply because a friend mentioned reading Middlemarch, and I remembered quoting George Eliot’s novel in a blog post, and that post turned out to be this one.
Had somebody mentioned reading Herder, I might have recalled writing about him in a blog post; that would be this post too.
Our environment may influence our feelings, but what we make of those feelings is up to us. Thus we are free; we are not constrained by some fixed “human nature”—or if we are, who is to say what its limits are?
Rembrandt van Rijn (and Workshop?), Dutch, 1606–1669,
The Apostle Paul, c. 1657, oil on canvas,
Widener Collection, National Gallery of Art
This essay was long when originally published; now, on November 30, 2019, I have made it longer, in an attempt to clarify some points.
The essay begins with two brief quotations, from Collingwood and Pirsig respectively, about what it takes to know people.
The Pirsig quote is from Lila, which is somewhat interesting as a novel, but naive about metaphysics; it might have benefited from an understanding of Collingwood’s Essay on Metaphysics.
A recent article by Ray Monk in Prospect seems to justify my interest in Collingwood; eventually I have a look at the article.
Ideas that come up along the way include the following.
For C. S. Lewis, the reality of moral truth shows there is something beyond the scope of natural science.
I say the same for mathematical truth.
Truths we learn as children are open to question. In their educational childhoods, mathematicians have often learned wrongly the techniques of induction and recursion.
The philosophical thesis of physicalism is of doubtful value.
Mathematicians and philosophers who ape them (as in a particular definition of physicalism) use “iff” needlessly.
A pair of mathematicians who use “iff” needlessly seem also to misunderstand induction and recursion.
Their work is nonetheless admirable, like the famous expression of universal equality by the slave-driving Thomas Jefferson.
Mathematical truth is discovered and confirmed by thought.
Truth is a product of every kind of science; it is not an object of natural science.
The distinction between thinking and feeling is a theme of Collingwood.
In particular, thought is self-critical: it judges whether itself is going well.
Students of mathematics must learn their right to judge what is correct, along with their responsibility to reach agreement with others about what is correct. I say this.
Students of English must learn not only to judge their own work, but even that they can judge it. Pirsig says this.
For Monk, Collingwood’s demise has meant Ryle’s rise: unfortunately so since, for one thing, Ryle has no interest in the past.
In a metaphor developed by Matthew Arnold, Collingwood and Pirsig are two of my touchstones.
Thoreau is another. He affects indifference to the past, but his real views are more subtle.
According to Monk, Collingwood could have been a professional violinist; Ryle had “no ear for tunes.”
For Collingwood, Victoria’s memorial to Albert was hideous; for Pirsig, Victorian America was the same.
Again according to Monk, some persons might mistake Collingwood for Wittgenstein.
My method of gathering together ideas, as outlined above, resembles Pirsig’s method, described in Lila, of collecting ideas on index cards.
Our problems are not vague, but precise.
When Donald Trump won the 2016 U.S. Presidential election, which opinion polls had said he would lose, I wrote a post here called “How To Learn about People.” I thought for example that just calling people up and asking whom they would vote for was not a great way to learn about them, even if all you wanted to know was whom they would vote for. Why should people tell you the truth?
Polytropy 